フォント Computer Modern Typewriter Text Bold の METAFONT からの生成について

aghtex の \ttfamily 系フォント用に Computer Modern [1] の Typewriter Text 書体一式を METAFONT ソースを弄って生成したことについて。

• [1] Computer Modern - Wikipedia

★折角なので生成したフォントファイル (TTF形式) を aghtex_cmttxx10.zip においた。 フォント名から中身が分かるように以下の様に命名規則を定めた。

aghtex_cmFFBSDD.ttf

但し FF は書体を指定するアルファベット二文字で Typewriter Text の場合は tt ということにする。 B は太さを表し、細字なら l (light) 普通なら m (medium) 太字なら b (bold) 極太なら h (heavy) ということにした。 S は形状を表し、通常なら n (normal) 斜体なら s (slanted) イタリックなら i (italic) Small-caps なら c (caps) ということにした。 DD は整数で印刷する時に想定するポイント数で今回は 10 だけ調整込みで生成した。

★aghtex に組み込んだ。

\begin{tabular}{c||c|c}
\verb+\ttfamily+& 普通 & 太字 \\ \hline \hline
直立 & \ttfamily Hello world! & \ttfamily\bfseries Hello world! \\
斜体 & \ttfamily\slshape Hello world! & \ttfamily\bfseries\slshape Hello world! \\
イタリック & \ttfamily\itshape Hello world! & \ttfamily\bfseries\itshape Hello world! \\
Small-caps & \ttfamily\scshape Hello world! & \ttfamily\bfseries\scshape Hello world!
\end{tabular}

但し、aghtex では Small-caps はフォントではなくて CSS の font-variant-caps を使っている。 ところで実際にブラウザで試すと @font-face の font-style: italic と font-style: oblique のフォントは独立に設定できないようだ… (Chrome, Firefox, IE, Edge, WebKit で確認)。

前調査

段落モードでは1書体につき6字体必要

aghtex でも \ttfamily に対して $\LaTeX 既定の書体 Computer Modern Typewriter Text (cmtt) を使いたい。 記事 [2] でも述べたが $\LaTeX の段落モードでは family x series x shape の組み合わせでフォントを指定する。 新しく \ttfamily に対応するためには、(1 family につき) 2 series x 4 shapes = 8 種類のフォントが必要になる。 small-caps に関しては CSS の font-variant(-caps): small-caps を使うことにしても 2 series x 3 shapes = 6 種類のフォントが必要である。 一つ Regular なフォントを用意したら自動的に他を synthesize してくれたら良いのだが、 Web fonts の synthesize はブラウザによってまちまちなので、やはり自分で用意しなければならない。

• [2] Computer Modern (AMSFonts) のファイル名と中身の対応表 - TBD

Computer Modern Typewriter Text の足りない字体

先に調べた通り AMSFonts に付属している Computer Modern には cmtt (Computer Modern Typewriter Text) の太字版がない [2]。 一方で Computer Modern Unicode (CMU) [3] には太字と太字イタリックや細字斜体などがある。 しかし太字斜体がどこにもない。 自分で作るしかないのかなと考える。一応 FontForge (フォント編集ソフト) [4] に輪郭を太らせる機能があることは知っている。

• [3] Computer Modern Unicode fonts
• [4] FontForge Open Source Font Editor

Computer Modern は METAFONT で定義されている

元々 Computer Modern は METAFONT で書かれた [1] そうだ。 CMU のページによると CMU も METAFONT ソースから生成しているそうなので CMU のソースを確認してみる。 色々調べた結果、恐らく CMU におけるフォント生成手順は以下のようになっている。

CMU におけるフォント生成手順 for Typewriter Text の Bold (Bold Italic)

1. ectb.mf (ectx.mf): CMU のソースに含まれるファイル。これが Bold (Bold Italic) のアルファベットの METAFONT ソースである。
2. ectb.pfb (ectx.pfb) 生成: 上のファイルを mftrace に入れて得られる。 mftrace の中では一旦 mf で字形をラスタライズして、その輪郭を autotrace というプログラムでなぞらせて PostScript を生成している。 その PostScript を t1asm などのコマンドを用いて Type 1 (Binary) 形式のフォントファイルに変換する。
3. cmuntb.sfd (cmuntx.sfd) 生成: 上のファイル + 他の文字 (ギリシャ文字やその他のヨーロッパ文字) を含むファイル ??tb.pfb (??tx.pfb) をくっつけて FontForge ファイルを生成する。
4. cmuntb.ttf (cmuntx.ttf) 生成: 最終的なフォントファイル。

METAFONT について調べる [5,6]。 昨今一般的なアウトラインフォントではなくストロークフォントの様だ。 つまり、字形の輪郭ではなくて字画の中心線の情報を保持する。 但し、ペンの形状などを指定することができる。 METAFONT はテキスト形式のプログラムになっていて人の手で記述できるようになっているようだ。 "一次連立方程式を解いてくれる" 機能もあって、 CAD みたいに点の関係を与えるだけで方程式を解いて位置を確定してくれる。

• [5] METAFONT - Wikipedia
• [6] 今さら人に聞けないMETAFONT - Qiita

CMU の ectb.mf の中を覗くとパラメータの設定だけして他の mf を呼び出している。

% ectt.mf
%
%%%%中略(パラメータの設定)%%%%
generate exroman %%%%<-他のmfを呼び出している?%%%%

endinput;

AMSFonts に含まれる tt のソースも複数確認してみたが似たような形である。 つまり一連の Computer Modern のフォントは、文字の定義は全て一括で行っていて、 但しパラメータを変えて様々なスタイルの字形を生み出しているということらしい。 つまり、このパラメータを弄るだけで好きな太さ・形状の Computer Modern フォントを生成できるのでは。

METAFONT を生成して ttf に変換する

スクリプトを書いて生成を行った。 生成するだけならば以下のような雰囲気でできる (コマンドはお使いの環境に合わせて適宜解釈して下さい)。

$ sudo dnf install texlive mftrace
$ git clone git@github.com:akinomyoga/aghfonts.git
$ cd aghfonts
$ ./generate_ttfamily.sh

以下はスクリプトの中でやっていること。

1 パラメータを線形補外して *.mf を自動生成する

Computer Modern のソースにはパラメータがたくさんある。 "文字の太さ" みたいな分かりやすいパラメータはなくて、 字体各部分に対応する値を1つ1つ手で調整する。気が遠くなる。

面倒なので手に入るソースに現れるパラメータ値の差分を取って、 線形補間・補外してパラメータを決定することにした。以下のソースを元にする。

• amsfonts/cm/cmtt*.mf (Typewriter Text Regular),
• cm-unicode-0.7.0/ectb.mf (Typewriter Text Bold),
• cm-unicode-0.7.0/ectx.mf (Typewriter Text Bold Italic),
• amsfonts/cm/cmtcsc10.mf (Typewriter Text Small-caps)

注意点としては ectb.mf 及び ectx.mf に書き込まれているパラメータ値は fontsize 10 の時だけしか調整されていないということ。 他の fontsize の値は Regular な Typewriter Text の時の値と同じになっている。

適当にスクリプトを書いてmfを生成する。 以下のような感じの .mf ファイルを {細字, 通常, 太字, 極太} ✕ {通常, 斜体, イタリック, Small-caps} ✕ {8pt, 9pt, 10pt, 12pt} で 4x4x4 = 64 種類生成した。

% THIS IS UNOFFICIAL COMPUTER MODERN SOURCE FILE cmtt10.mf BY K MURASE.
% IT MUST NOT BE MODIFIED IN ANY WAY UNLESS THE FILE NAME IS CHANGED!

% Computer Modern Typewriter Text for use with 10 point
if unknown cmbase: input cmbase fi

font_identifier:="AGHTEX_CMTTBC"; font_size 10pt#;

u#:=21.0/36pt#;                            % unit width
%%%%%%%%%%%%
%%%%中略%%%%
%%%%%%%%%%%%
 lower.fudge:=0.8;                   % factor applied to weights of heavy characters

%------------------------------------------------------------------------------

generate csc                    % switch to the driver file

2 mftrace で *.mf から *.ttf に変換する

CMU に倣って mftrace で *.pfb を生成したい。Fedora に mftrace を入れた。

$ sudo dnf install mftrace

mftrace を genfonts.sh の真似をして呼び出してみる。 しかし t1asm でエラーになって動かない。t1utils を reinstall しても変わらない。 使い方が悪いのかと思って色々やったが Ubuntu に mftrace を入れてみると普通に動いた。 結局、t1utils [7] をソースから自分でビルドして入れたら Fedora でも動くようになった。

$ git clone git@github.com:kohler/t1utils.git
$ cd t1utils
$ autoreconf -i
$ ./configure --prefix=$HOME/opt/t1utils
$ make install
$ ln -s ~/opt/t1utils/bin/t1asm ~/bin/

• [7] kohler/t1utils: Utilities for manupulating Adobe Type 1 font software

単に mftrace --formats=ttf example.mf としたら mf から ttf ファイルを直接生成してくれた。

3 FontForge スクリプトでメタ情報埋め込み

完成したファイルを見るとフォントのメタ情報が色々欠けているので、 コマンドラインで設定できるツールを探す。 Perl で書かれた FontUtils というのがあるらしいが結局どうやって入れたら良いのか分からなかったのでやめた。 検索すると Windows で使える ttfname3 [9,10] というのがあったようだがソースコードが見つからなかったので Linux では使えない。 あと、XML なので操作を書くのが面倒だ。

• [8] FontUtils
• [9] メイリオ・meiryoKe・ttfname3
• [10] ttfname3

結局 FontForge スクリプト [11] で処理することにした。 ついでに自動ヒントなども付加するようにしてみる。

• [11] Writing scripts to change fonts in FontForge

以下は実際にシェルスクリプトで FontForge スクリプトを呼び出している部分を抜粋したもの (勿論各シェル変数には適切な値が設定されている)。

fontforge -lang=ff -script <<EOF
Open("$input")
SetFontNames("$key", "$ttffamily", "$ttffull", "$ttfsub", "$copy", "$version")
#CIDSetFontNames("$key", "$ttffamily", "$ttffull", "$ttfsub", "$copy")
SetTTFName(0x409, 0, "$copy")
SetTTFName(0x409, 1, "$ttffamily")
SetTTFName(0x409, 2, "$ttfsub")
SetTTFName(0x409, 3, "$ttfid")
SetTTFName(0x409, 4, "$ttffull")
SetTTFName(0x409, 5, "Version $version")
SetTTFName(0x409, 13, "The SIL Open Font License, Version 1.1.")
SetTTFName(0x409, 14, "http://scripts.sil.org/OFL")
SetOS2Value("Weight", $os2weight)
#SetOS2Value("StyleMap", $os2style)

# Automatical Adjustment
SelectWorthOutputting()
CanonicalContours()
CanonicalStart()
#ClearHints()
#AutoHint()
#AutoInstr() #自動ヒンティング命令を出力すると表示が変なのでoff

Generate("$output", "ttf", 0x200, -1)
EOF

FontForge の関数一覧はページ [12] にある。SetTTFName で設定する値についてはページ [13] を参照した。 FontForge による自動ヒンティング命令を出力するとレンダリング結果がおかしいので、ヒンティング命令は出力しないことにした。

• [12] Scripting functions
• [13] Developer Resources

結果

以下は自分のディスプレイ用の ClearType の画像なので、他のディスプレイだと色がついたり滲んだり掠れたりして見えるかもしれない。

通常 (上から Light, Medium, Bold, Black)

aghtex Computer Modern Typewriter Text Regular

斜体 (上から Light, Medium, Bold, Black)

aghtex Computer Modern Typewriter Text Oblique

イタリック (上から Light, Medium, Bold, Black)

aghtex Computer Modern Typewriter Text Italic

Small-caps (上から Light, Medium, Bold, Black)

aghtex Computer Modern Typewriter Text Small-caps

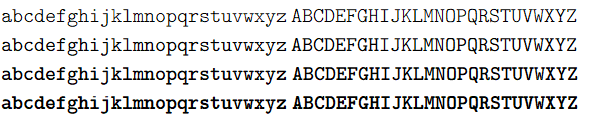
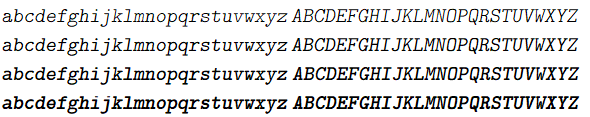
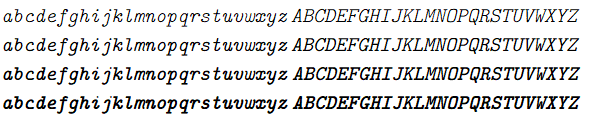
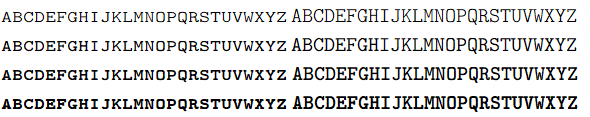
最後に

普段なら適当に調べるだけ調べて「将来的なメンテナンスのコストと見返り」などなど考えて諦めるところだが、記事 [1] にしてしまったので中途半端は駄目な気がしてフォント作成までしてしまった。書いて思うのはフォント作成よりも記事執筆の方が時間がかかる。しかし、アウトプットは大切な気がする。時間を無駄にした気もするし、しかしこういった時間の使い方も大切にしなければならないとも思う。

アウトプットには時間がかかる。成果を上げることを考えていると、すぐに簡単にアウトプットできないくらいに成果が溜まってしまう。そう考えると研究も本当は一日でできる程度の内容に留めて、一日の研究成果を時間をかけて論文にする、というぐらいがバランスが良いのかもしれない。

C++: private メンバにアクセス - テンプレート明示的実体化の時に private メンバのポインタが取れる

C++ Advent Calendar を見たら private メンバにアクセスする記事が2日連続している [1,2]。 記事 [1] は自前のライブラリを使っていて説明は別記事で行っている [3]。 記事 [3] では2つの方法について言及していて、friend によるものと明示的テンプレート実体化によるものだそうだ。しかし具体的な説明は更に別の記事を参照している。 記事 [2] は本気なのかネタなのか #define private public である (使い古されたネタなのである)。

• [1] AdC2019 C++ 6日: ブログズミ: [C++] 本当に private なところ
• [2] AdC2019 C++ 7日: C++部・ユニットテストの裏技 〜private関数をテストする〜 - Qiita
• [3] ブログズミ: [C++] Private な関数のテスト

明示的実体化による方法が具体的にどういうものなのか気になったので調べてみた。 序でなので別の方法についてもまとめる。

• 【2019-12-08】非公開記事の wayback machine 上のアーカイブへのリンクを追記
• 【2019-12-09】privateメンバへアクセスするコードの調査 - Qiita に詳しい考察があります!

テンプレートの明示的実体化を使う手法

しかし記事 [3] で紹介されているリンク [4] を見ると「非公開に設定されています」となって見られない (追記: Wayback Machine にアーカイブが残っていた)。検索すると英語の記事が見つかった [5]。

• [4] privateメンバに外部から非侵入的にアクセスする - redboltzの日記 (Archive)
• [5] litb's Blog: Access to private members. That's easy!

コードを読んでみると「テンプレートの明示的実体化のテンプレート実引数で private メンバポインタが取得できる」[10] ということを利用しているようだ。知らなかった。

• [10] C++17 N4659 [temp.explicit]/12

自分でやってみる

元の記事 [5] のコードはもっと単純化できそうなので自分でやってみる。 取り敢えずターゲットは以下のクラスのデータメンバ A::a。

class A { int a = 12345; }

こんな感じにしたらアクセスできる (wandbox):

int A::*memptr;
template<int A::*mp> struct Initializer { inline static auto dummy = memptr = mp; };
template struct Initializer<&A::a>;

int main() {
  A obj;
  std::cout << obj.*memptr << std::endl;
}

使いやすいようにまとめてみる

毎回記述するのは面倒なのでまとめる (wandbox):

// 準備
namespace TBD {
  template<typename MemPtr, typename Tag>
  struct accessor {
    inline static MemPtr ptr;
    template<MemPtr mp> struct init { inline static auto dummy = ptr = mp; };
  };
}

// 使う時
using A_a = TBD::accessor<int A::*, struct tag_a>;
template struct A_a::init<&A::a>;
int main() {
  A obj;
  std::cout << obj.*A_a::ptr << std::endl;
}

マクロにしてしまった方が楽かもしれない

余り使いたくないけれども、マクロの方がすっきりするかも (wandbox):

// 準備
#define TBDDeclareMemberPointer(MemPtr, Name, Member) \
  using TBDAccessType_##Name = MemPtr; \
  static TBDAccessType_##Name Name; \
  template<TBDAccessType_##Name value> struct TBDAccessFiller_##Name { inline static auto dummy = Name = value; }; \
  template struct TBDAccessFiller_##Name<&Member>;

// 使う時
TBDDeclareMemberPointer(int A::*, memptr, A::a);
int main() {
  A obj;
  std::cout << obj.*memptr << std::endl;
}

この方法だと依存クラスに対する処理を書けない (明示的実体化を依存文脈に書けない為)。 しかし、テストが目的だとすれば結局全て明示的に書くことになる気がするので余り気にならないのだろう。 いざ必要になれば我慢して使う。

他の手法

序でに、他にどのような方法があったかまとめ。

1 #define private public ✕

これは冗談の域を出ない。色々な悪いことが起こりそうなのは想像に難くない。そもそも、

class A { int a; }

のような定義の private メンバに関しては効果がない。 だからと言って #define class struct も追加すると今度は

template<class T> void f() {}

の様な記述をしていた時にコンパイルできなくなる。

更に記事 [6] に

• [6] privateメンバの合法的アクセス - ぐるぐる～

さらに予約語を#defineするのは非合法でもある。

と書かれている。例によってリンク先 [7] が非公開に設定されているが、検索すると規格の [macro.names]/2 に記述がある様だ。

• [7] 低学歴無能俸給生活者の日記＞＜ (Archive)
• [8] Redefine(#define) reserved c++ key word - Stack Overflow
• [9] C++17 N4659 [macro.names]/2

2 friend を設定する ○

これが一番自然な方法だろう。但し、これは対象本体に手を入れなければならない。

本体を弄れない時にどうするか。 記事 [6] で紹介している Exceptional C++ Style 15章 では、 自分で偽物のヘッダを作って"偽装" しているそうだ。 でもそれだと匿名名前空間で定義されているクラスなどに対して使えない。更に ODR 違反である。

3 同じレイアウトのクラス型に reinterpret_cast する ✕

これも Exceptional C++ Style 15章 にあるそうだ [6]。 然し、これは標準レイアウトクラスでなければ動作を保証できない。一般には未定義の動作である。

4 テンプレート特殊化を利用する △

これも Exceptional C++ Style 15章 から [6]。 対象クラスに関数テンプレートメンバがあれば、その関数テンプレートの特殊化を作成してその中でメンバにアクセスすることができる。 しかし、関数テンプレートメンバがなければ使えない手法である。単純なクラスの場合大抵は関数テンプレートメンバはない。

Computer Modern (AMSFonts) のファイル名と中身の対応表

$\LaTeX で使われている Computer Modern (AMSFonts) のファイル名を見ても中身が分からない。開いて確かめた結果を記録する。

1 Introduction

動機: \tt (Computer Modern 等幅) の太字や斜体はあるのだろうか?

aghtex は数式モードでは $\LaTeX の既定のフォントである Computer Modern を主に使っている。特に TeX 環境に付属している AMSFonts (SIL Open Font License) [1] に含まれているものを Type 1 から Web fonts の形式に変換している。一方で、段落モードでは Computer Modern は使わずに OS のフォントを使う様にしている。

• [1] CTAN: Package amsfonts

しかしやはり、段落モードでも特に \tt については Computer Modern を使いたい気がする。しかし問題は Web fonts だと (Firefox でしか) font-synthesis が有効にならないこと *1。つまり、font-weight や font-style を指定しても太字や斜体にならない。これに対応する為には太字版や斜体版の Web fonts を一つ一つ用意しなければならない。そもそも Computer Modern (AMSFonts) に \tt の太字版や斜体版はあるのだろうか。

Computer Modern (AMSFonts) のファイル名は謎

Computer Modern を確認する。 Computer Modern (AMSFonts) の実体は /usr/share/texmf/fonts/type1/public/amsfonts/cm 的な場所にある。ファイル名は

cm(略号)(数字).pfb

の形式をしている。(数字)の部分はそのフォントのポイント数、つまり、どのポイント数で印刷されることを想定しているかである (Computer Modern では印刷する時の大きさに合わせて文字のバランスを微妙に変えている)。 一方で (略号) はそれぞれ何を意味しているのかすぐには分からない。 検索しても説明は見つからない。開いてみないと分からない。 結局 \tt の太字版があるかどうか全て開いて確認する羽目になった。 二度と全部開いて確かめるということはしたくないのでここにまとめておく。

因みに cmextr や cm-super もファイル名だけ眺めてみたが、どれも cm にあったのと同じの気がしたので中は確認しなかった。

$\LaTeX のフォントの分類

$\LaTeX の段落モードのフォントは family と series と shape の組み合わせで指定する。

• family には既定で \rmfamily (セリフ rm = roman), \sffamily (サンセリフ sf = sans-serif), \ttfamily (等幅 tt = typewriter text) がある。
• series には \bfseries (太字 bf = boldface), \mdseries (普通 medium) がある。
• shape には \upshape (直立体 up = upright), \slshape (斜体 sl = slanted), \itshape (イタリック it = italic), \scshape (small-caps) がある。

論理上は 3 x 2 x 4 = 24 の組み合わせがあることになるが、実際には全てに異なる字体が用意されている訳ではない。 何れにしても、この 3 x 2 x 4 に従って Computer Modern のファイルたちを並べてみたい。

ところで、書いていて「そういえば tt って何で tt なんだろう」と思ったけど、たぶん teletype のことの気がする。と思っていたら typewriter text っぽい。

2 対応表

どうも文章を書くと無駄な事を書き始めて良くない。完全に蛇足である。動機とか背景とか重要性とかを説明したくなる。というかですね、そもそも見た目が論文みたいである。今気づいたけれど、引用を [番号] にして下部にリスト表記したくなるのもそれだ。

2.1 rm 系のフォント

	通常	太字
直立	cmr, cmex	cmb, cmbx
斜体	cmsl	cmxsl
イタリック	cmmi, cmti	cmmib, cmxti
Small-caps	cmcsc	N/A

• イタリックで cmmi は数式用で cmti がテキスト用であろう。数式用の方が微妙に幅に余裕を持って設計されている。また数式用ではアルファベットのにがイタリックであるが、テキスト様では数字や記号も含めてイタリックになっている。
• 他に cmdunh という縦長の字形の入ったフォントファイルがあった。
• また、cmu は字形はイタリックだが直立したものである。

2.2 tt 系のフォント

tt 系のフォントには太字は用意されていない様子である。

	通常	太字
直立	cmtt, cmtex	N/A
斜体	cmsltt	N/A
イタリック	cmitt	N/A
Small-caps	cmtcsc	N/A

他に cmvtt というファイルがあって開いてみると横長の tt に見える。v という名前から推測するに縦書き用だろうか?

2.3 sf 系のフォント

sf 系のフォントは余り用意されていない。

	通常	太字	極太
直立	cmss	cmssdc	cmssbx
斜体	cmssi	N/A	N/A
イタリック	N/A	N/A	N/A
Small-caps	N/A	N/A	N/A

他に cmssq 及び cmssqi というのがあって、これらはそれぞれ cmss 及び cmssi の丸ゴシック的変種に見える。

2.4 cmf?

cmf? という系列があった。微妙に手書きっぽいが serif っぽくもある変な字体である。

	通常	太字
直立	cmff	cmfib
斜体	cmfi	N/A

2.5 mathcal

cmsy 及び cmbsy (太字) は mathcal 及びその太字である。

	通常	太字
直立	cmsy	cmbsy

3 最後に

結論: \tt の太字はない。斜体やイタリックはある。

フォントファイルを開いて中を確認しただけでそれっぽい記事が出来上がって自分でも驚いている。 研究もこんな感じに文章を書くだけでできたらいいんだけれど。研究はファイルを開くのとは違って簡単じゃない。

余談: Variable フォント

この記事のために調べていたら variable フォントというものがあるらしい。凄い。style や weight 毎に何個ものフォントファイルがあるのは不毛だと思っていたが、parametrized されたフォントの仕様があるのだ。macOS も Windows も freetype も既に対応しているらしい?

• [2] Variable フォントガイド - CSS: カスケーディングスタイルシート | MDN
• [3] Variable Fontを試して使おう！Font Playground - bagelee（ベーグリー）
• [4] The Typekit Blog | バリアブルフォント – 柔軟なデザインを可能にする新しい種類のフォント

余談: Computer Modern Unicode

以下のページから Computer Modern の Typewriter Text の Bold や Bold Italic がダウンロードできる。 しかしライセンス的にどうだろう。"Free for commercial use" と書いてあるけれど本当だろうか。このサイト自体が怪しい。

• [5] Computer Modern Font Family · 1001 Fonts

追記: 以上でダウンロードできるのは cm-unicode (Computer Modern Unicode; CMU) というプロジェクト [6] のファイルの様だ。 正式リリース 0.6.3 のライセンスは X11 License で、開発版 0.7.0 (2009年を最後に止まっている) のライセンスは SIL Open Font License (OFL) だそうだ。 開発版は SourceForge のサイト [7] からダウンロードできる。

• [6] Computer Modern Unicode fonts
• [7] Computer Modern Unicode fonts - Browse /cm-unicode at SourceForge.net

*1:最近確かめていないので、もしかすると最近は他のブラウザもできるようになっているかもしれない。

はてなブログでスクリプトを一斉適用する方法

はてなブログで全てのページにスクリプトを埋め込む方法。少なくとも２つ世に出回っているようだ。最初、MathJax 関連で検索して当たった記事 [1] の方法を使って記事 [2] の <script> を埋め込んでいた (以下 "方法2") のだが、コメントで n7shi さんに正当な方法 (以下 "方法1") があることを教えてもらった。

• [1] はてなブログで数式を書く方法(mathjaxの導入) - shangtian’s blog
• [2] aghtex4hatenablog: はてなブログの数式を aghtex で表示する - TBD

1 方法1 (推奨)

一番自然な方法。[右上のメニュー]-[設定]-[詳細設定]-[headに要素を追加]の欄にスクリプトタグを記述すれば良い。

[右上のメニュー]-[設定]

[詳細設定]

[headに要素を追加] (結構下の方にある)

設定画面を見ると meta タグを埋め込むのが本来の目的のように見えるが、公式 [3] も「スクリプトを自由に記述できます」と書いているので気兼ねせずスクリプトを埋め込める。

• [3] ブログのhead部分にmetaタグなどを自由に追加できるようにしました - はてなブログ開発ブログ

2 方法2 (非推奨)

[右上のメニュー]-[デザイン]-[カスタマイズ]-[ヘッダ]-[タイトル下] にスクリプトタグを記述する方法。

[右上のメニュー]-[デザイン]

[カスタマイズ]-[ヘッダ]-[タイトル下]

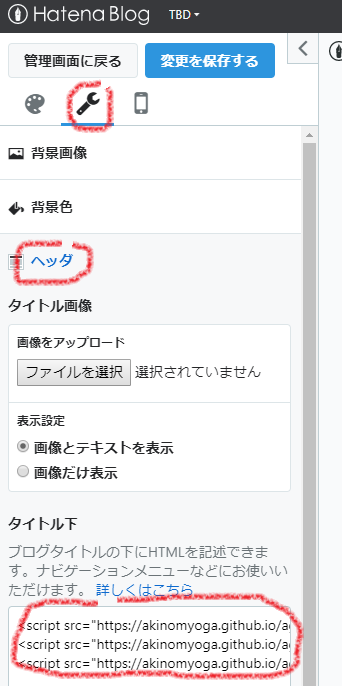しかし、どうもスマホで見るとスクリプトが埋め込まれていない。

2.1 スマホ用の設定は別

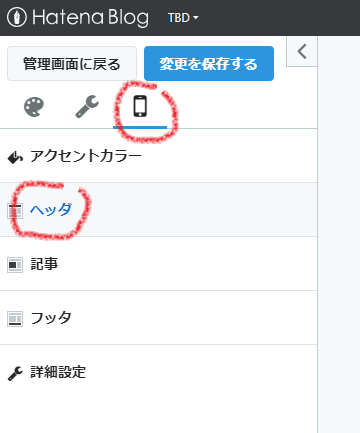
デザイン設定の画面を見るとスマホ用の設定が存在する。 なるほど、PC用の設定とスマホ用の設定は別なのかと思って、同様にヘッダのタイトル下を見てみると…

[スマホ]-[ヘッダ]

[タイトル下]

"はてなブログPro" という文字が見える。え、スマホでスクリプトを設定するのは有料なの??

2.2 "レスポンシブデザイン" にチェックを入れたら動いた

無料でやるには個別のページにスクリプトを毎回埋め込むしかないのかな…

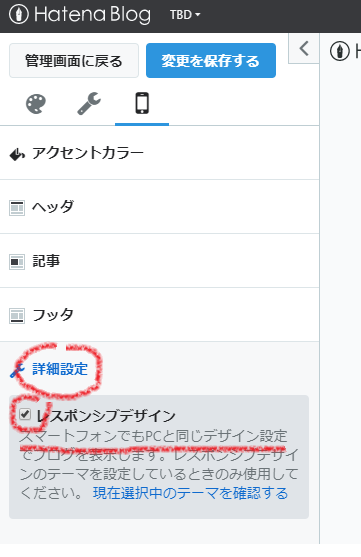
と思っていたら別の設定が [詳細設定] にあった。以下の様に [レスポンシブデザイン] というところに "スマートフォンでもPCと同じデザイン設定" と書かれている。チェックを入れてみたらスマホでも PC 用に設定した <script> が読み込まれるようになった。

[詳細設定]

aghtex4hatenablog: はてなブログの数式を aghtex で表示する

はてなブログの数式は使いにくい。 記事 [1] のコメントで n7shi さんに「数式にMarkdownやはてなキーワードの処理が入り込んで」ということを指摘してもらった。 実際にはてなブログで数式を色々書いてみると確かに段々とこれが気になってきた。 先ず ] を含む $\TeX コードを指定する方法が分からない (→n7shi さんのコメント参照: \\] とすれば良いそうだ。というか記事 [2] にもちゃんと書いてあった…)。それがなくてもいろいろ回避するために書き方を変えるのは疲れる。

• [1] はてなブログを数式のあるメモに使ってみるの事 - TBD
• [2] はてなブログで数式を書く - 七誌の開発日記

n7shi さんの最近の記事を見るとどうやらはてなブログの MathJax ではなくて K%{\KaTeX}% を自前で呼び出して数式を表示しているようだ [3]。 自分で数式の表示処理を呼び出した方がいろいろ制御できるから便利なのである。

• [3] KaTeXのテスト - 七誌の開発日記

ところではてなブログでは は記事の最初の方に [tex:～] がないと有効にならないらしい。 →別の理由だった。このページの下の補足を参照のこと。

1 顛末: aghtex を使いたい

どうせ他のライブラリを自分で呼び出すとなれば、やはり aghtex を使いたい。aghtex は10年ぐらい前から作っている自前の$\LaTeX表示ライブラリ (github.com/akinomyoga/agh) [4]。MathJax や K%{\KaTeX}% などは数式部分だけの変換を目的としたものだが、aghtex は元々 *.tex の文書全体の変換を目的としたものなので、paragraphモードのコマンドも使えるし、式番号も生成できるし、式へのリンクも生成できる。

• [4] akinomyoga/agh: Ageha JavaScript Library

追記: MathJax でも式番号自動生成とリンクをできるらしい [5]。

• [5] Automatic Equation Numbering — MathJax 3.0 documentation

1.1 はてなブログのスタイルシートと干渉する問題

しかし実際に aghtex を使ってみると表示が滅茶苦茶になってしまう。どうやらはてなブログの設定している CSS で .entry-content table {...} だとか .entry-content table td {...} だとかいうものがあって、それが aghtex の生成する <table> や <td> のスタイルを上書きしてしまうという事が起こっている様だ。こういう事は一般に起こりうる問題であると前々から認識していたが、できるならばここで根本的な対策をしておきたい。

• (没案1) 対策として <table> や <tr> や <td> を使わずに適当な要素に display: inline-table; や display: table-row; や display: table-cell; を指定するように書き換えてみたら colspan や rowspan が効かなくなってこれはこれで駄目だ。調べると display: table-cell; で colspan, rowspan を使う方法は存在しないようだ。何のための display: table-cell; なのか、という気がしないでもない。
• (没案2) CSS の詳細度を色々弄って何とかならないかと考えたが、親ドキュメントで #id table td などとやられた日には、詳細度で勝つために動的に CSS を生成しなければならない。そもそも、CSSの詳細度は設計が根本的に狂っている。広まってしまったので今から仕様を変える訳にも行かないのだろう。
• 結局 !important で逃げるしかないという事になった。!important を使うと今までの詳細度による計算が変わってしまう (全てに !important をつければ今までと変わらないのかもしれないがそれは嫌だ。!important は最低限にしたい)。動かなくなるといけないので慎重に書き換えなければならない。結局 aghtex を整理しながら大幅に手を入れることになった。取りあえず今のところは動いている。

1.2 MathJax や K%{\KaTeX}% には \multicolumn がない?

しかし MathJax や K%{\KaTeX}% がはてなブログのスタイルシートの影響を受けていないのは何でだろう。table を使っていないのだろうか。だとすれば colspan や rowspan を使わずに色々実現しているのだろうか。例えば \multicolumn をどうやって実現するんだろう (座標を計算して絶対配置するしかない?) と思って、確認しようとしたらどうやら MathJax も K%{\KaTeX}% も \multicolumn に対応していないようだ。aghtex は勿論 \multicolumn に対応している。ちゃんと動いている。

\begin{pmatrix}
  a & b & c \\
  \multicolumn{3}{c}{ABC} \\
  d & e & f
\end{pmatrix}

\begin{pmatrix} a & b & c \\ \multicolumn{3}{c}{ABC} \\ d & e & f \end{pmatrix}

1.3 はてなブログの処理と干渉しない記法?

はてなブログの数式の問題点は、「Markdownやはてなキーワードの処理」による干渉を避けるために煩雑な書き方をしなければならなかったことである。 つまり「Markdown やはてなキーワードの処理」が入らない様に $\TeX ソースを指定できれば良いのである。 `～` や ```～``` を使って、特定の条件で変換を適用することにした。Qiita が ```math ～``` でやっているのと同じ作戦。

2 使い方

はてなブログの側に色々コードを埋め込むのは面倒なので agh.fly.js に新しくはてなブログ専用の処理を追加することにした。

2.1 ロード

以下の3行を埋め込めば aghtex がはてなブログ用にロードされる。

<script src="https://akinomyoga.github.io/agh/agh.js?20191202c"></script>
<script src="https://akinomyoga.github.io/agh/agh.lang.tex.js?20191202c"></script>
<script src="https://akinomyoga.github.io/agh/agh.fly.js?20191202c#hatena"></script>

常用するにははてなブログの [設定]-[詳細設定]-[headに要素を追加] の欄に上記スクリプトを記述すれば良い[6, 7方法1]。最初、記事[8, 7方法2]の方法を使っていたが、後で記事[7]のコメントで n7shi さんにより良い方法を教えてもらった。

• [6] ブログのhead部分にmetaタグなどを自由に追加できるようにしました - はてなブログ開発ブログ
• [7] はてなブログで数式を書く方法(mathjaxの導入) - shangtian’s blog
• [8] はてなブログ(無料)でスマホでもスクリプトを一斉適用する - TBD

2.2 インライン数式

インライン数式の記法として

$`～`

を採用することにした。これははてなブログ的には $<code>～</code> という形に変換されて、中身「～」にはMarkdownやはてなキーワードの変な処理は入らない。

普通の記述の仕方

$～$

にも対応している。中に他と干渉しそうな記述がなければこちらでも良い。

以下の記述方法にも対応している。

<span class="aghtex">～</span>

2.3 独立した数式

独立行の数式のためには以下の記法を使う。

```tex:環境名
～
```

環境名は align, align*, equation, eqnarray など任意の環境名。これも中身「～」には変な処理は入らない (はず)。

他に以下にも対応している。\begin{align}～\end{align} で囲んで変換される。

<div class="aghtex">
～
</div>

2.4 プリアンブル

プリアンブルに指定したい内容 (\usepackage や \def や \newcommand など) は以下の形式で指定する。

```tex:preamble
～
```

3 サンプル

3.1 "KaTeXのテスト - 七誌の開発日記" の例

数式の例として記事 [3] のものを試させてもらうことにした。 こうして3種類の数式表示エンジンを並べてみると楽しい。 この例の範囲内では aghtex は少なくとも K%{\KaTeX}% と同程度には速い。元々 MathJax は遅いのである。

• MathJax では です。
• aghtex では $c=\pm\sqrt{a^2+b^2} です。
• K%{\KaTeX}% では K%{c=\pm\sqrt{a^ 2+b^ 2}}% です。

MathJax	aghtex	K%{\KaTeX}%
\[x=\frac{-b±\sqrt{b^2-4ac}}{2a}\] \[f(x)=\frac1{\sqrt{2πσ^2}}\exp\left(-\frac{(x-μ)^2}{2σ^2}\right)\] \[i\hbar\frac∂{∂t}ψ=\left(\frac{(-i\hbar∇)^2}{2m}+V\right)ψ\] \[rC=\frac{∂C}{∂t}+\frac12σ^2S_t^2\frac{∂^2C}{∂S_t^2}+rS_t\frac{∂C}{∂S_t}\]	x=\frac{-b±\sqrt{b^2-4ac}}{2a} f(x)=\frac1{\sqrt{2πσ^2}}\exp\left(-\frac{(x-μ)^2}{2σ^2}\right) i\hbar\frac∂{∂t}ψ=\left(\frac{(-i\hbar∇)^2}{2m}+V\right)ψ rC=\frac{∂C}{∂t}+\frac12σ^2S_t^2\frac{∂^2C}{∂S_t^2}+rS_t\frac{∂C}{∂S_t}	x=\frac{-b±\sqrt{b^2-4ac}}{2a} f(x)=\frac1{\sqrt{2πσ^2}}\exp\left(-\frac{(x-μ)^2}{2σ^2}\right) i\hbar\frac∂{∂t}ψ=\left(\frac{(-i\hbar∇)^2}{2m}+V\right)ψ rC=\frac{∂C}{∂t}+\frac12σ^2S_t^2\frac{∂^2C}{∂S_t^2}+rS_t\frac{∂C}{∂S_t}

3.2 意味のある数式の例

記事 [9] の数式。正しいかは知らない。

• [9] Dentonの式の縮退のある場合 - TBD

  \left\|
    \begin{pmatrix} v_{i_1,j_1} \\ v_{i_2,j_1} \\ \vdots \\ v_{i_\Lambda,j_1} \end{pmatrix}
    \wedge \dots \wedge
    \begin{pmatrix} v_{i_1,j_P} \\ v_{i_2,j_P} \\ \vdots \\ v_{i_\Lambda,j_P} \end{pmatrix}
  \right\|^2
  &= \frac{\displaystyle
    \sum_{j_{P+1} < \dots < j_\Lambda\atop \{j_p\}_{p=1}^P \cap \{j_p\}_{p=P+1}^\Lambda = \emptyset}
    \prod_{k=1}^{n-\Lambda}[\lambda - \lambda_k(M_{j_1,\dots,j_\Lambda})]
  }{\displaystyle
    \prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]} \\
  &= \frac{c_{n-\Lambda}\{\lambda - \lambda_k(M_{j_1,\dots,j_P})\}_{k=1}^{n-P}}{
    \displaystyle
    \prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]}.

3.3 式の参照のテスト

式$\eqref{eq:sample3-eq1}$は足し算です!
```tex:align
  A = B + C. \label{eq:sample3-eq1}
```

式$\eqref{eq:sample3-eq1}$は足し算です!

  A = B + C. \label{eq:sample3-eq1}

3.4 着色のテスト

```tex:preamble
\usepackage{color}
```
```tex:align
  \textcolor{red}{A} = \textcolor[rgb]{0.0,0.5,0.0}{B} + \textcolor{blue}{C}.
```

\usepackage{color}

  \textcolor{red}{A} = \textcolor[rgb]{0.0,0.5,0.0}{B} + \textcolor{blue}{C}.

3.5 DOM要素埋め込みのテスト

aghtex が MathJax や K%{\KaTeX}% に勝っていると思うのは aghtex は DOM 要素を含められるということ。 これが可能なのは aghtex は自身では具体的なレイアウト計算はしていなくて全てブラウザのレイアウトエンジンに要素の配置を計算させているから。 数式の中に含まれているDOM要素の大きさなどが動的に変わってもそれに応じて数式が変形する。 実際に使える場面があるのかは不明だけれども。

<div class="aghtex">
x &= \sqrt{
  \left[
  <table style="margin:0;display:inline-table;vertical-align:middle;">
  <tr><td>A</td><td>B</td></tr>
  <tr><td>C</td><td>D</td></tr>
  </table>\right]_{A=123}^{456}
  + \frac{<code>code block</code>}{<a href="https://katex.org/">K%{\KaTeX}%</a>}
  + <button>Button</button>
}
</div>
<script>
(function() {
  var button1 = document.getElementById("button1");
  agh.addEventListener(button1, "click", function() {
    console.log("button1 clicked");
    button1.innerHTML = "Button Clicked!";
    button1.style.height = "100px";
  });
})();
</script>

x &= \sqrt{ \left[

A	B
C	D

\right]_{A=123}^{456} + \frac{code block}{K%{\KaTeX}%} + Button }

最後に

よく考えたら、はてなブログを使ってみたのはデフォルトで数式を表示する機能があるらしいということが分かったから。 自分で数式を表示するコードを書いてメンテナンスするのは面倒だし、下手に自由度があるので数式の表示についていろいろ工夫が始まってしまう。 初めからある機能しか使わないことにすれば数式表示関連で色々と工夫して時間を費やしてしまうこともなくなる。

そう思っていたはずなのに、結局 aghtex に手を出してそれに時間を費やしているので、はてなブログを使い始めた意味がないのでは。。

でも結果には満足している。特に式番号を自動で生成できるのは便利である。

補足: はてなブログでは <pre> の直後で数式記法が効かなくなる

以下のように <pre> を直接記述すると数式記法 [tex:～] が効かなくなるということが判明した。

<pre>hello</pre>
[tex: c = \pm \sqrt{a^ 2+b^ 2}]

以下のように ```～``` を間に挟むと動くようになるようだ。

<pre>hello</pre>
<div style="display:none;">
```dummy
```
</div>
[tex: c = \pm \sqrt{a^ 2+b^ 2}]

Dentonの式の縮退のある場合

Qiitaの記事 [1] を見た。どうやら「固有値だけから固有ベクトルが求められる」という arXivの論文 [2] が話題になっていたようだ。件の式 (記事[1]に倣ってDentonの式と呼ぶことにする) は以下の形をしている。

\newcommand{\adj}{\mathrm{adj}}

  |v_{i,j}|^2 \prod_{k=1\atop k\neq i}^{n} [\lambda_i(A) - \lambda_k(A)] = \prod_{k=1}^{n-1}[\lambda_i(M) - \lambda_k(M_j)].

但し、$A$は$n\times n$行列で、$\lambda_k(X)$ は行列 $X$ の $k$ 番目の固有値で、$v_{i,j}は$A$の固有値 $\lambda_i(A)に対応する固有ベクトル$v_iの第 $j$ 成分。$M_jは$A$から$j$行目と$j$列目を抜き去って作られる小行列。ちゃんとみると、その行列の固有値だけでなく小行列の固有値も要求しているので、論文のタイトルは扇動的である。

縮退がある場合には両辺0になる

そもそもこの式が気になった理由は、もしかすると自分の計算で使っている固有ベクトル(応力主軸)を求めるコードの問題を解決するのに使えるかもしれないと思ったから。自分の計算で問題が起こるのは対称性によって縮退がある場合と、それからブロック対角になっている場合。その対策に少し計算量の多いことをしている。その観点でDentonの式を見ると、どうも縮退がある場合には両辺が0になってしまって固有ベクトルに関する情報は何も得られない。使えない。

縮退がある場合の類似の関係式?

縮退がある場合にも何か類似の関係式があると考えるのが自然な気がする。然し、縮退がある場合にはユニタリ変換の自由度があるので固有ベクトルの組は一意に定まらない。従って、単純に固有ベクトルの各要素について情報が得られるとは考えにくい。何らかのユニタリ不変な組み合わせに対して何か言わなければならない。と思ったがゴールの形もないのに闇雲に考えてもよく分からない。

方針を変えて縮退のない場合の導出を観察してそれを拡張する。

関係式1

余因子行列(adjugate)による導出の拡張で以下が得られる。固有値 $\lambda$ に対して、

  \sum_{k=1\atop \lambda_k(A)= \lambda}^n |v_{k,j_1}|^2
  = \frac{\sum_{j_2 < \dots < j_\Lambda\atop j_p\neq j_1 (p=2,\dots,\Lambda)}
  \prod_{k=1}^{n-\Lambda}[\lambda - \lambda_k(M_{j_1,\dots,j_\Lambda})]
  }{\prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]}. \label{eq:r1}

但し、$\Lambda は $\lambda の重複度で、 $M_{j_1,\dots,j_\Lambda} は行列 $A$ から($j_1行$,\dots,j_\Lambda行$,j_1列$,\dots,j_\Lambda列)を除いて得られる小行列。

Proof.

余因子行列と逆行列の関係から、

  \adj(\lambda - A + \epsilon)
  &= (\lambda - A + \epsilon)^{-1} \det(\lambda - A + \epsilon) \\
  &= \left(\sum_{k=1}^n \frac1{\lambda - \lambda_k(A) + \epsilon} v_k v_k^\dag\right) \det(\lambda - A + \epsilon).
%  &= \left(\sum_{k=1\atop \lambda_k(A)= \lambda}^n \frac1\epsilon v_kv_k^\dag
%    + \sum_{k=1\atop \lambda_k(A) \neq \lambda}^n \frac1{\lambda - \lambda_k(A)+\epsilon}v_kv_k^\dag\right) \\
%  &\qquad\times \epsilon^\Lambda\prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A) + \epsilon] \\

但し、面倒なので $\lambda I_n - A$ などは $\lambda - A$ と書いている。 右辺の $\epsilon$ の最低次を見ると

\epsilon^{\Lambda-1} \left(\sum_{k=1\atop \lambda_k(A)= \lambda}^n v_kv_k^\dag\right)
    \prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]

になっている。特に対角成分$(j_1,j_1)$を見れば

\epsilon^{\Lambda-1} \left(\sum_{k=1\atop \lambda_k(A)= \lambda}^n |v_{k,j_1}|^2\right)
    \prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]

一方で、左辺の該当する次数の係数を微分して取り出すと、

  &\left. (\Lambda-1)!
  \frac{\partial^{\Lambda-1}}{\partial\epsilon^{\Lambda-1}}
  \adj(\lambda - A + \epsilon)_{j_1j_1}\right|_{\epsilon=0} \\
  &\qquad= \sum_{j_2 < \dots < j_\Lambda\atop j_p\neq j_1 (p=2,\dots,\Lambda)}
  \det(\lambda - M_{j_1,\dots,j_\Lambda}) \\
  &\qquad= \sum_{j_2 < \dots < j_\Lambda\atop j_p\neq j_1 (p=2,\dots,\Lambda)}
  \prod_{k=1}^{n-\Lambda}[\lambda - \lambda_k(M_{j_1,\dots,j_\Lambda})].

■

関係式2

関係式$\eqref{eq:r1}$は或いはまた以下のようにも書ける。

  \sum_{k=1\atop \lambda_k(A)= \lambda}^n |v_{k,j_1}|^2
  = \frac{c_{n-\Lambda}\{\lambda - \lambda_k(M_{j_1})\}_{k=1}^{n-1}
  }{\prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]}. \label{eq:r2}

但し、$c_k\{a_i\}_{i=1}^n は $\{a_i\}_{i=1}^n の $k$ 次基本対称式。

Proof.

関係式1の導出で左辺 $\adj(\lambda - A + \epsilon)_{j_1j_1} = \det(\lambda - M_{j_1} + \epsilon)$ の $\epsilon^{\Lambda-1}$ 次の係数は、$\lambda - M_{j_1}$ の特性多項式の $\Lambda - 1$ 次の係数なので、$\lambda - M_{j_1}$ の固有値の $\Lambda - 1$ 次の基本対称式になっている。■

関係式3

Cauchy-Binet型公式による導出 [2,3] の拡張で以下が得られる。

\left|\det\begin{pmatrix}
  v_{i_1,j_1} &\cdots &v_{i_\Lambda,j_1} \\
  \vdots & \ddots & \vdots \\
  v_{i_1,j_\Lambda} &\cdots &v_{i_\Lambda,j_\Lambda}
\end{pmatrix}\right|^2 = \frac{
  \prod_{k=1}^{n-\Lambda} [\lambda - \lambda_k(M_{j_1,\dots,j_\Lambda})]
  }{\prod_{k=1\atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]}. \label{eq:r3}

但し、$i_1,\dots,i_\Lambda は固有値$\lambda$に属する相異なる固有ベクトルの番号である。 また、$j_1,\dots,j_\Lambda ($1\le j_p\le n)は相異なる整数。

Proof.

原論文 [2] に倣って $v_{n-\Lambda+1},\dots,v_n$ が固有値 $\lambda$ の固有ベクトルとする。 $B$ として $(n-\Lambda)\times n$ 行列を考えて、

  |\det\bigl(\begin{array}{cccc}B&v_{n-\Lambda+1}&\dots&v_n\end{array}\bigr)|^2 \cdot \prod_{i=1}^{n-\Lambda} \lambda_k(A) = \det(B^\dag AB)

を得る。$B = \begin{pmatrix}0\\\\I_{n-\Lambda}\end{pmatrix}$ を考えれば直ちに

  \left|\det\begin{pmatrix}
    v_{n-\Lambda+1,1} &\cdots &v_{n,1} \\
    \vdots & \ddots & \vdots \\
    v_{n-\Lambda+1,\Lambda} &\cdots &v_{n,\Lambda}
  \end{pmatrix}\right|^2
  \prod_{k=1}^{n-\Lambda} [\lambda - \lambda_k(A)]
  &= \det(\lambda - M_{1,\dots,\Lambda}) \\
  &= \prod_{k=1}^{n-\Lambda} [\lambda - \lambda_k(M_{1,\dots,\Lambda})].

■

関係式4?

関係式$\eqref{eq:r1}$,$\eqref{eq:r2}$と関係式$\eqref{eq:r3}$の間を無理やり埋めると次の式が成り立ちそうな気がする。

  &\left\|
    \begin{pmatrix} v_{i_1,j_1} \\ v_{i_2,j_1} \\ \vdots \\ v_{i_\Lambda,j_1} \end{pmatrix}
    \wedge \dots \wedge
    \begin{pmatrix} v_{i_1,j_P} \\ v_{i_2,j_P} \\ \vdots \\ v_{i_\Lambda,j_P} \end{pmatrix}
  \right\|^2 \nonumber \\
  &\qquad= \frac{\displaystyle
    \sum_{j_{P+1} < \dots < j_\Lambda\atop \{j_p\}_{p=1}^P \cap \{j_p\}_{p=P+1}^\Lambda = \emptyset}
    \prod_{k=1}^{n-\Lambda}[\lambda - \lambda_k(M_{j_1,\dots,j_\Lambda})]
  }{\displaystyle
    \prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]} \\
  &\qquad= \frac{c_{n-\Lambda}\{\lambda - \lambda_k(M_{j_1,\dots,j_P})\}_{k=1}^{n-P}}{
    \displaystyle
    \prod_{k=1 \atop \lambda_k(A) \neq \lambda}^n [\lambda - \lambda_k(A)]}.

但し、$\wedge は外積。$1 \le P \le \Lambda$ で、$j_1,\dots,j_P は相異なる整数 ($1\le j_p \le n)。

面倒になったので上の式が本当に成立するかどうかは誰か別の人が屹度考えてくれる。

最後に

縮退がある場合でも成立する関係式が得られた訳だが、これが実際に自分の数値計算に使えるかというと、使えない。 小行列の固有値を求めるのは大変だし、求められたとしても位相の情報が完全に欠落している。 縮退がある場合の判定に使う閾値の調整も大変だし、閾値付近で不連続な振る舞いが出ないかもちゃんと確認しなければならない。

現在使っている方法は $\adj(\lambda - A)$ の列ベクトルの中でノルム最大の物を選ぶという方法であり、 そちらの方が断然簡単である。$3\times3$ という小さな行列なので $\adj$ を直接求めるコストも小さい。

今後、Dentonの式がもっと使いやすい形に発展していく可能性はあるだろうか。

参照

• [1] 話題の「固有値から固有ベクトルを求める」を検証する - Qiita
• [2] [1908.03795] Eigenvectors from Eigenvalues
• [3] デントンとテレンスタオの論文を読み解く、その１ - ほんまにコメントほしい 日本語による証明の説明はここに。

指数型分布族の共役事前分布

最大エントロピー原理関連で指数型分布族を検索してみたら記事 [1] で

主な特徴として、ベイズ統計において、これらの分布は共役事前分布をもつことが上げられます。

と書かれている。少し考えてみる。指数型分布族では確率密度は以下のように記号的に書ける*1。

\Pr(x|\theta)dx = \frac1{Z(\theta)}e^{-\theta\cdot Q(x)}d\mu(x).

但し $Z(\theta)$ は規格化で $\mu$ は何か積分測度。

共役事前分布

$x$ を観測した時の事後確率は以下の形になる。

\Pr(\theta|x)
  \stackrel{\theta}{\propto} \Pr(x|\theta)\Pr(\theta)
  \stackrel{\theta}{\propto} \frac1{Z(\theta)}e^{-\theta\cdot Q(x)}\Pr(\theta).

何だか分からない。$x_1,\dots,x_n$ を観測したらこうなる。

\Pr(\theta|x_1,\dots,x_n)
  \stackrel{\theta}{\propto} e^{-\theta\cdot \textstyle\sum_{i=1}^n Q(x_i) - n\ln Z(\theta)}\Pr(\theta).

要するに と のところを、共役事前分布のハイパーパラメータにすれば良いのだ。という訳で共役事前分布は以下のように定めれば良さそう。

\Pr(\theta|\bar Q, \nu) d\theta = \frac1{N(\bar Q, \nu)} e^{-\nu [\bar Q\cdot \theta + \ln Z(\theta)] } d\mu_0(\theta).

但し、 はハイパーパラメータ $(\bar Q, \nu)$ に依らないパラメータ空間の測度で好きに設定できる。$N(\bar Q, \nu)$ は規格化定数。

ハイパーパラメータの更新式については自明と思ったが時間が経つとまた分からなくなるので書いておく。$x$ を測定したとき、以下のようにすれば良い。

  \nu' &= \nu + 1, \\
  \nu' \bar Q' &= \nu \bar Q + Q(x).

思ったこと

呆気ない。よくある説明は分布毎に共役事前分布を書き下しているから気が付かないけれど、このようにして見ると指数型分布族の共役事前分布は大したことない。共役事前分布は結局「電荷の期待値 $\bar Q$」と「自信 $\nu$ (これまでの試行回数)」の情報だけしか持っていないんだなと。。

共役事前分布の式の形を見るとこれはどうもエントロピーの形である。特に $\theta$ を最尤推定で決めれば、指数の肩は大偏差関数であり、熱力学的エントロピーである。$\nu\to\infty$ は無限回試行の極限であり、熱力学的極限である。ルジャンドル変換は示強変数$\theta$→示量変数 $\langle Q\rangle$ の逆写像を考える。ベイズの定理はパラメータ → 確率変数 の条件付き確率を逆転させて尤度関数にする。ヘルムホルツ自由エネルギーもしくは圧力は読み替えの時の再規格化から出てくる。何だか分からなくなってきた。この辺りの関係は今ひとつ分かっていない。後で考える機会があったら考える。

ところで指定された分布族に対して共役事前分布って測度 $\mu_0(\theta)$ を除けば一意なんだろうか。と最後に思った。

参照

• [1] 指数型分布族とは？定義と性質をわかりやすく解説 | 全人類がわかる統計学

更新記録

• 修正 (2019-11-27): 測度 $\mu_0(\theta)$ 依存性の明示
• 追記 (2019-11-27): 指数型分布族一般形について脚注
• 追記 (2019-11-27): ハイパーパラメータ更新式

*1:一般には $\theta\cdot Q(X)$ の部分は $\Phi(\theta)\cdot Q(X)$ の形らしいが、それって $\theta' := \Phi(\theta)$ に変数変換して必要があれば拘束条件をかけてパラメータ空間を制限するだけの気がするので、$\theta\cdot Q(X)$ を標準形として問題ない気がする。拘束条件は後述の $\mu_0(\theta)$ に担わせれば良い。